The Story of Joon

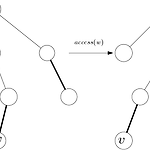
Link/Cut Tree (1) 앞선 포스트에서 LCT에 대한 기본적인 내용을 다루었는데, 이번 포스트에서는 LCT가 어떻게 활용될 수 있는지 간단하게만 알아보려고 한다. 보충 자료 같은 느낌의 포스트이다. 1. Link 연산의 확장 원래의 Link 연산은 붙이는 쪽이 represented tree의 루트인 경우에만 가능했다. 그러나 실제로 루트가 아닌 노드를 붙이고 싶을 때도 있을 것이다. 이를 위해서는 represented tree의 루트를 변경하는 작업이 필요하다. 어떤 represented tree의 한 노드를 $v$라고 했을 때, access($v$)를 하면 v에서 루트로 연결되는 preferred path가 생긴다는 점은 이전 포스트에서 알아보았다. 그런데 여기서 주목할 점은 이 preferr..

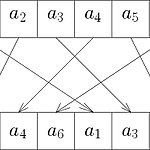
고속 푸리에 변환(Fast Fourier Transform, FFT)은 convolution을 $O(N\log N)$에 구할 때 활용된다. 이 포스트에서는 코드 자체보다도 FFT 알고리즘의 원리를 알아보는 것이 목적이다. 코드만 보고싶다면 맨 아래로 내려가면 된다. 푸리에 변환은 수학에서 매우 중요한 개념이며 공학 분야에서도 중요하게 다루어진다. 일반적으로 푸리에 변환은 함수를 함수로 보내는 변환인데, PS에서 활용되는 푸리에 변환은 수열을 수열로 보내는 이산 푸리에 변환(Discrete Fourier Transform, DFT)이다. 주기가 $N$인 수열 $\lbrace a_j\rbrace_{j=0}^{N-1}$의 DFT $\lbrace A_n\rbrace_{n=0}^{N-1}$은 다음과 같이 정의된다..

Link/Cut Tree (2) 다음 자료들을 참고했다. * 위키피디아 링크 * MIT Lecture Note Link/Cut Tree를 이해하거나 구현하기 위해서는 먼저 Splay Tree에 대한 이해가 필요하다. Splay Tree에 대한 내용은 여러 곳에 잘 설명되어 있다. Link/Cut Tree는 여러 개의 트리를 관리하는 자료구조이다. 이 자료구조의 특징은, find_root(노드가 속한 트리의 루트), link(한 트리의 루트를 다른 트리의 노드로 연결), cut(루트가 아닌 노드와 부모 사이의 연결 제거) 연산을 모두 amortized $O(\log N)$의 복잡도에 수행이 가능하다는 것이다. 앞서 말했듯이 LCT는 여러 개의 트리로 되어있는데, 이 각각의 트리를 represented tr..

cubelover님의 블로그를 많이 참고했다. Splay Tree에 대한 설명은 이 블로그로 가면 많은 도움이 된다.