The Story of Joon
Linear Algebra in Problem Solving (3) 본문
Linear Algebra in Problem Solving (1)
Linear Algebra in Problem Solving (2)
Linear Algebra in Problem Solving (3) (현 포스트)
기존 두 포스트에서는 선형대수학에 등장하는 기본적인 행렬 연산과 행렬에 관련된 중요한 식을 어떻게 효율적으로 계산하는지에 대해 알아보았다. 하지만 PS에서 대놓고 이런 값을 구하라고 요구하는 문제는 드물고, 보통 선형대수학을 응용해야 하는 문제가 나오게 된다. 대표적인 예시가 1편에서 나왔듯이 XOR을 \(\mathbb{F}_2\)에서 벡터의 덧셈으로 생각하는 방식이다. 이 포스트에서는 좀더 고급 응용인, 조합론에서 선형대수학이 응용되는 예시를 다룬다.
이분 그래프의 인접 행렬
PS는 물론이고 CS와 이산수학 전반적으로 매우 중요한 대상인 그래프는 수학적으로 인접 행렬(adjacency matrix)로 많이 표현된다. 이는 간단히 말해 각 행과 각 열이 그래프의 정점을 나타내고, \(i\)번 정점에서 \(j\)번 정점으로 가는 간선이 있을 경우 \((i, j)\) 위치에 1이 적혀 있고 그렇지 않을 경우 0이 적혀있는 그래프이다.
이분그래프(bipartite graph)에서도 비슷한 형태의 행렬(biadjacency matrix라고도 불린다)이 정의 가능한데, 각 행이 첫 번째 정점 집합에 속한 정점, 각 열이 두 번째 정점 집합에 속한 정점일 때 마찬가지로 대응되는 두 정점이 연결되어 있는지 여부에 따라 1 또는 0이 적혀있는 행렬이다. 첫 번째 정점 집합과 두 번째 정점 집합의 크기가 같을 경우 이 행렬의 행렬식은 이 이분 그래프의 완전 매칭(perfect matching)의 개수와 연관이 있다. \(n\times n\) 정사각행렬 \(A\)의 행렬식의 정의를 다시 살펴보자.
\[\det(A)=\sum_{\sigma\in S_n}\left(\operatorname{sgn}(\sigma)\prod_{i=1}^n a_{i,\sigma_i}\right)\]
\(A\)가 이분 그래프의 인접 행렬이라면 \(a_{i,\sigma_i}\)들의 곱은 첫 번째 집합의 정점 \(i\)와 두 번째 집합의 정점 \(\sigma_i\)가 모든 \(i\)에 대해 연결되어 있을 때만 1이 된다. 이러한 \(\sigma\)는 완전 매칭을 나타낸다는 것을 알 수 있다. 따라서 위 행렬식의 정의에서 0이 아닌 항은 정확히 완전 매칭의 개수만큼 남아있게 된다.
하지만 공교롭게도 \(\operatorname{sgn}(\sigma)\)의 존재 때문에 행렬식이 완전 매칭의 개수가 되지는 못한다. 완전 매칭의 개수와 같아지는 식은 다음과 같이 permanent라는 식이 있다.
\[\operatorname{per}(A)=\sum_{\sigma\in S_n}\prod_{i=1}^n a_{i,\sigma_i}\]
\(A\)가 이분 그래프의 인접 행렬일 때 이 식은 정확히 완전 매칭의 개수와 같아진다. 그러나 아쉽게도 이 식은 행렬식처럼 다항 시간에 구할 수 있는 방법이 알려지지 않았다. 인접 행렬의 경우처럼 행렬의 모든 원소가 0 또는 1인 경우에조차 #P-complete이며, 이는 NP-complete보다 어렵다는 뜻이다. 따라서 다항 시간 알고리즘을 찾으려는 시도는 하지 않는 것이 좋다.
아쉬운 대로 행렬식을 이용해 완전 매칭의 개수의 홀짝성 정도는 알 수 있다. \(\mathbb{F}_2\)에서는 1과 -1이 같기 때문이다. 만일 홀수라는 결론(즉 \(\mathbb{F}_2\)에서 1)을 얻었다면, 완전 매칭의 개수가 0은 아니라는 뜻이므로 적어도 하나의 완전 매칭의 존재가 보장된다. 하지만 짝수라는 결론을 얻었다고 해서 완전 매칭이 존재하지 않는 것은 아니므로, 단순히 존재성 판단 용도로 사용하기에는 흔한 이분 매칭 알고리즘보다 나을 것이 전혀 없다.
일반적인 그래프의 인접 행렬
이분 그래프의 인접 행렬의 행렬식은 (완전히 만족스럽지는 않지만) 완전 매칭의 개수와 관련이 있음을 알아보았다. 일반적인 그래프의 경우 인접 행렬의 행렬식에 직관적인 의미를 부여하기는 쉽지 않다. 순열의 cycle decomposition을 이용하는 것이 한 가지 방법인데, 행렬식의 정의를 구성하는 각 항은 어떤 순열 \(\sigma\)에 대하여 행렬의 \((i, \sigma_i)\) 위치의 원소들의 곱이라는 것을 생각해 보자. 이 순열 \(\sigma\)를 cycle decomposition 하고 나면 각 cycle은 그래프에서의 cycle과 대응된다.
예를 들어 아래와 같은 (유향) 그래프를 생각해 보자.

이 그래프의 인접 행렬은 아래와 같이 나타난다.
\[\begin{bmatrix}0&\color{red}{1}&1&0&0\\0&0&\color{red}{1}&0&0\\ \color{red}{1}&0&0&1&0\\0&0&0&0&\color{red}{1}\\1&0&0&\color{red}{1}&0\end{bmatrix}\]
여기서 붉은 표시한 숫자들을 가리키는 순열을 그래프에서 대응시킨 것이 위 그래프에서 붉은 간선들이다. 즉 행렬식을 구성하는 각 항이 그래프의 사이클 분해에 대응된다는 것을 알 수 있다.
이 자체로는 큰 의미를 찾기 어렵지만, 인접 행렬의 행렬식이 그래프의 사이클과 관련이 있다는 점을 이용해 사이클이 개수가 적거나 특수한 구조를 가진 그래프의 인접 행렬을 효율적으로 구하는 PS 문제가 Open Cup과 같은 대회에서 종종 출현한다. 예시는 아래 연습문제에서 찾아볼 수 있다.
Lindström–Gessel–Viennot lemma
줄여서 LGV라고 많이 부르는 이 보조정리는 특정 조건을 만족하는 경로 조합의 가짓수를 셀 때 이용된다. 행렬식의 흥미로움을 맛볼 수 있는 재미있는 예시이다. 아래와 같이 출발지 4개와 도착지 4개가 있는 길이 복잡하게 얽혀 있다고 생각해 보자. 각 \(i\)에 대해 \(i\)번 출발지에서 \(i\)번 도착지로 이어지는 네 개의 경로를 만들려고 하는데, 경로는 무조건 오른쪽(+x 방향)으로만 향하고 경로끼리 교차하지 않게 하고 싶다. 모두 몇 가지 방법이 있을까?
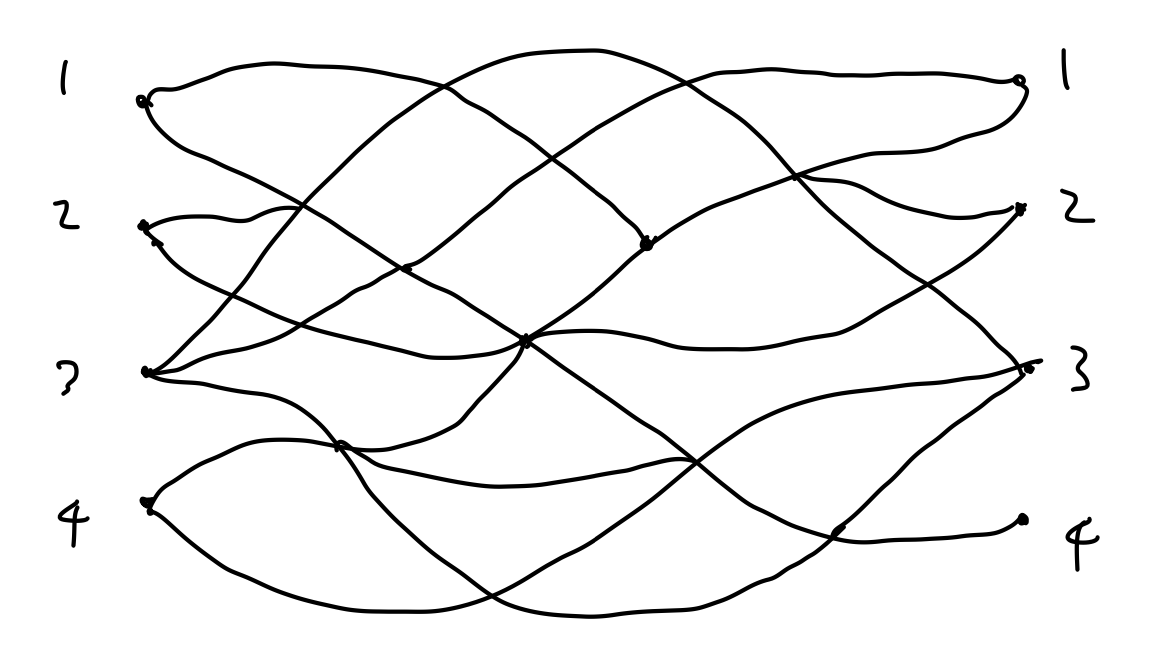
예를 들어 아래와 같은 경로 조합이 가능하다.

반면 아래 경로 조합은 교차했기 때문에 탈락이다.
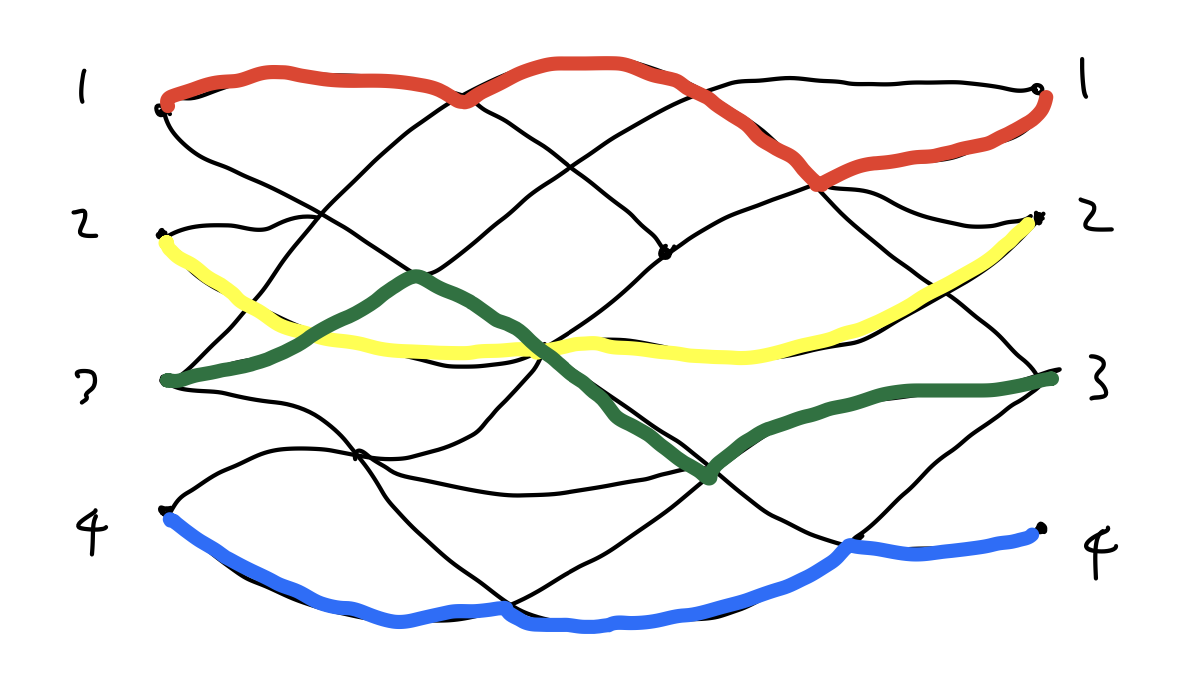
컴퓨터의 도움이 있다면, 단순히 \(i\)번 출발지에서 \(j\)번 도착지로 가는 경우의 수 \(a_{ij}\)는 다이나믹 프로그래밍으로 어렵지 않게 구할 수 있을 것이다. 만일 겹치지 않아야 한다는 조건이 없다면 \(a_{11}\)부터 \(a_{44}\)까지 모두 곱하면 그만이다. 하지만 교차하는 경로 조합은 세어서는 안되기 때문에 빼줘야 한다. 이걸 어떻게 할 수 있을까?
LGV에 의하면, 놀랍게도 아래 행렬의 행렬식이 우리가 원하는 경우의 수와 같아진다.
\[A=\begin{bmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{bmatrix}\]
이는 더욱 일반적인 상황에서도 성립한다. \(n\)개의 출발지와 \(n\)개의 도착지가 있는 directed acyclic graph (DAG)가 있다고 하자. 교차하지 않는 (하지만 출발지와 도착지의 번호가 다를 수 있는) 모든 경로 조합 \(P\)에 대해, \(i\)번 출발지에서 출발했을 때 어떤 도착지에 도착하냐에 따라 순열 \(\sigma(P)\)를 만들 수 있다. 다시 말해 \(i\)번 출발지에서 출발하면 \(\sigma(P)_i\)번 도착지에 도착한다. 이때 \((i, j)\) 위치에 \(i\)번 출발지에서 \(j\)번 도착지로 가는 경로의 수를 넣은 행렬 \(A\)에 대해 다음이 성립한다.
\[\det(A)=\sum_{P:\text{non-intersecting path tuple}}\operatorname{sgn}(\sigma(P))\]
이는 다음과 같이 쓸 수도 있다. 어떤 순열 \(\sigma\)에 대해 \(i\)번 출발지에서 출발해 \(\sigma_i\)번 도착지에서 도착하는 교차하지 않는 경로 조합의 가짓수를 \(c(\sigma)\)라고 하면, 아래 식이 성립한다.
\[\det(A)=\sum_{\sigma:[n]\to[n]}\operatorname{sgn}(\sigma)c(\sigma)\]
위의 예시에서는 겹치지 않는 경로 조합이 가능한 경우가 \(i\)번에서 출발해 \(i\)번에 도착하는 경우밖에 없기 때문에 이 식에서 \(\sigma\)가 항등함수인 경우만 남아서 성립하게 된다.
이제 이런 일이 벌어지는 이유를 알아보도록 하자. 일반적인 경우를 논하기 전에, 가장 간단한 \(n=2\)인 경우를 먼저 보면 도움이 된다. 이 경우 행렬식이 아래와 같다.
\[\det(A)=a_{11}a_{22}-a_{12}a_{21}\]
\(a_{11}a_{22}\)가 나타내는 수는 교차를 고려하지 않고 1, 2번 출발지에서 출발해 순서대로 1, 2번 도착지에 도착하는 경우의 수이고, \(a_{12}a_{21}\)이 나타내는 수는 교차를 고려하지 않고 1, 2번 출발지에서 출발해 순서대로 2, 1번 도착지에 도착하는 경우의 수다. 즉 이 행렬식이 우리가 원하는 식과 같아진다는 의미는 이 두 식에서 카운팅한 교차하는 경로의 수가 상쇄된다는 의미이다! 아래 그림을 보자.

왼쪽은 \(a_{11}a_{22}\)에서 카운팅하는 교차 경로 조합이고, 오른쪽은 \(a_{12}a_{21}\)에서 카운팅한 교차 경로 조합인데, 이 둘은 행렬식에서 부호가 반대가 되기 때문에 상쇄되어 최종 식에서 나타나지 않게 된다.
이 상황을 좀더 일반화하면 우리가 카운팅하기 원하지 않는 경로 조합을 부호가 반대인 것끼리 짝지어서 상쇄시킬 수 있다. 핵심 아이디어는, 교차점에서 둘의 진행방향을 한번 바꿔주는 것이다. 위의 \(n=4\)인 경우에서 탈락했던 예시를 다시 한번 보자. 그냥 \(a_{11}\cdots a_{44}\)를 계산하면 이 예시까지 카운팅하게 된다. 이를 상쇄시키기 위해 처음으로 생긴 교차점에서 둘의 진행 방향을 바꿔 보자. (개미 문제를 풀어본 경험이 있다면 이 '진행 방향을 바꾸는' 아이디어가 좀더 와닿을 수 있다.)
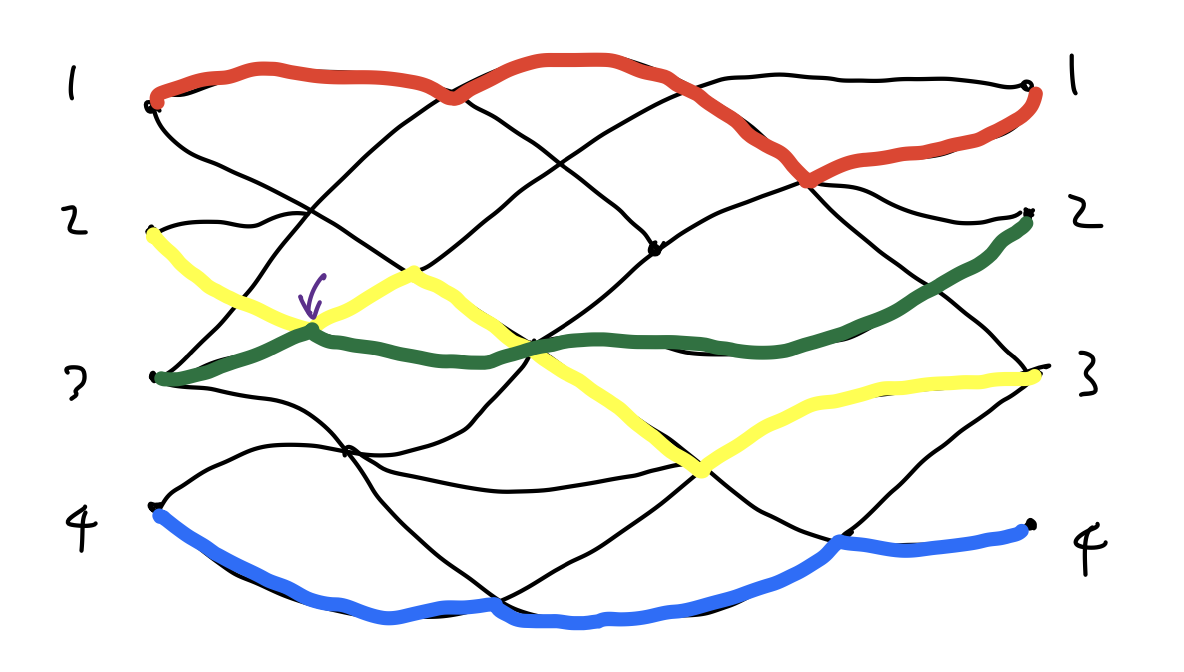
이 예시 역시 탈락해야 할 경로 조합으로, 위의 예시와 짝지어 보자. 진행 방향을 한번 바꿨기 때문에 이 바뀐 경로 조합을 카운팅하는 순열은 원래 순열과 홀짝성이 달라지게 된다. 이는 다시 말해 \(\operatorname{sgn}\)의 부호가 뒤집힌다는 뜻이므로, 행렬식에서 두 예시가 상쇄되어 우리의 목적을 달성하게 된다.
이렇게 교차점이 있는 경로 조합들은 짝지어서 모두 없앨 수 있고, 결국 교차점이 없는 경로 조합만 최종 식에 남아있게 된다.
LGV는 Young tableaux라는 것의 개수를 세는 문제에도 활용될 수 있는데, 자세한 내용은 생략한다. 관심 있는 독자는 위키피디아를 읽어보면 잘 설명되어 있다.
지금까지는 경우의 수를 세는 문제와 연관짓기 위해 LGV의 특수한 경우를 설명했다. 아주 약간 더 일반적인 형태는, 그래프의 간선에 가중치 \(w:E(G)\to\mathbb{R}\)가 주어져 있는 형태이다. (가중치는 대부분 독자에게 익숙한 실수 \(\mathbb{R}\)을 사용했지만, 아무 ring을 써도 상관없다.) 이 경우 어떤 경로(혹은 경로 조합)의 가중치는 그 경로(혹은 경로 조합)에 있는 간선의 가중치의 곱으로 정의하고, \(a_{ij}\)는 \(i\)번 출발지에서 \(j\)번 도착지로 가는 경로의 수 대신 \(i\)번 출발지에서 \(j\)번 도착지로 가는 모든 가능한 경로들의 가중치의 합으로 정의한다. 그러면 LGV는 다음과 같은 형태가 된다.
\[\det(A)=\sum_{P:\text{non-intersecting path tuple}}\operatorname{sgn}(\sigma(P))w(P)\]
우리가 논의한 내용은 모든 가중치가 1인 특수한 경우이다. 증명은 특수한 경우와 완전히 동일하다.
Cauchy–Binet formula
Cauchy–Binet formula는 두 행렬의 곱으로 나타내는 정사각행렬의 행렬식을 구하는 방법에 관한 식이다. \(A\)가 \(n\times m\) 행렬이고 \(B\)가 \(m\times n\) 행렬일 때, 두 행렬의 곱 \(AB\)의 행렬식을 아래와 같이 구할 수 있다.
\[\det(AB)=\sum_{I\subseteq{[m]\choose n}}\det(A_{[n],I})\det(B_{I,[n]})\]
식이 익숙하지 않은 독자를 위해 간단히 설명하면, \([m]=\{1,\cdots,m\}\)의 모든 크기 \(n\)짜리 부분집합 \(I\)에 대해, \(A\)에서 번호가 \(I\)에 들어있는 열벡터를 모은 정사각행렬의 행렬식과 \(B\)에서 번호가 \(I\)에 들어있는 행벡터를 모은 정사각행렬의 행렬식을 곱한 값을 모든 \(I\)에 대해 더하면 \(AB\)의 행렬식이 된다는 것이다.
이 식은 조합론에서 상당히 유명하고 중요한 식으로, 증명도 순수 대수적인 증명부터 조합적인 증명까지 매우 다양하다. 그중에서 대수와 조합을 모두 적절히 맛볼 수 있는 증명이 위의 LGV를 이용한 증명이다. (LGV를 C–B formala의 일반화로 볼 수도 있다.)
먼저 출발지 \(n\)개, 중간 경유지 \(m\)개, 그리고 도착지 \(n\)개를 만든다. 그리고 \(i\)번 출발지에서 \(j\)번 경유지로 가중치 \(A_{ij}\)인 간선을 연결하고, \(j\)번 경유지에서 \(k\)번 도착지로 가중치 \(B_{jk}\)인 간선을 만든다. 그러면 \(i\)번 출발지에서 \(k\)번 도착지로 가는 경로의 가중치 총합은 아래와 같이 나타나고, 이 값은 정확히 두 행렬의 곱 \(AB\)의 \(i,k\) 위치 원소이다. 그래프의 인접 행렬로 경로의 경우의 수 구하는 방식을 떠올리면 된다.
\[\sum_{j=1}^mA_{ij}B_{jk}\]
따라서 LGV에 의하면 \(AB\)의 행렬식에는 출발지에서 도착지까지 가는 교차하지 않는 않는 경로 조합으로만 이루어진 식이 남는다. 출발지의 집합을 \(S\) 도착지의 집합을 \(E\)라고 하면, 아래와 같다.
\[\det(AB)=\sum_{P:\text{non-intersecting path tuple } S\Rightarrow E}\operatorname{sgn}(\sigma(P))w(P)\]
교차하지 않는다는 것은, 경로 조합이 경유지를 정확히 \(n\)개 지난다는 의미이다. 이 경유지의 집합을 \(I\)라고 쓰면, 출발지에서 도착지까지의 경로 조합 \(P\)를 \(S\)에서 \(I\)까지의 경로 조합 \(P_1\)과 \(I\)에서 \(E\)까지의 경로 조합 \(P_2\)로 분해할 수 있다. 이때 중요한 것은 \(\operatorname{sgn}(\sigma(P))=\operatorname{sgn}(\sigma(P_1))\operatorname{sgn}(\sigma(P_2))\)가 성립한다는 것이다. (\(\operatorname{sgn}\) 함수가 순열의 곱셈을 보존하기 때문이다.) 따라서 위 식을 아래와 같이 다시 쓸 수 있다.
\[\sum_{I\subseteq{[m]\choose n}}\left(\sum_{P_1}\operatorname{sgn}(\sigma(P_1))w(P_1)\sum_{P_2}\operatorname{sgn}(\sigma(P_2))w(P_2)\right)\]
내부의 두 summation의 값은 (LGV에 의해, 혹은 자명하게) 각각 \(\det(A_{[n],I})\)와 \(\det(B_{I,[n]})\)가 되므로, 증명이 완료된다.
Matrix-tree theorem
위 Cauchy–Binet formula의 흥미로운 응용 중 하나가 바로 matrix-tree theorem이다. Matrix-tree theorem은 (무향) 그래프의 스패닝 트리의 개수를 쉽게 구할 수 있는 방법을 알려준다. 먼저 Laplacian matrix라는 것을 정의하는데, 정점의 개수가 \(n\)일 때 행렬의 \((i, j)\) 위치에 \(i=j\)이면 \(i\)번 정점의 차수, \(i\neq j\)이고 두 정점이 연결되어 있으면 \(-1\), 아니면 \(0\)이 들어있는 행렬이다. 아래와 같은 예시 그래프를 보자.

이 그래프의 Laplacian matrix는 아래와 같다.
\[L=\begin{bmatrix}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{bmatrix}\]
이제 matrix-tree theorem이 무엇인지 알아보자. 이 \(L\)에서 아무 행이나 하나 고르고 아무 열이나 하나 고른 후 그 행과 열을 삭제해서 \(3\times 3\) 행렬을 만든다. 아무거나 골라도 되지만, 간단하게 첫 번째 행과 첫 번째 열을 삭제하자.
\[L^*=\begin{bmatrix}3&-1&-1\\-1&3&-1\\-1&-1&2\end{bmatrix}\]
놀랍게도 이 행렬의 행렬식이 그래프의 스패닝 트리 개수와 같아진다.
이 결과 역시 잘 알려져 있고 다양한 증명이 존재하지만, 그중에서 위의 Cauchy–Binet formula를 이용한 증명을 소개하고자 한다. 이를 위해서는 \(L\)이 incidence matrix라는 것으로 분해될 수 있다는 것을 이해해야 한다. Incidence matrix는 adjacency matrix와 비슷하지만, 정점과 정점 사이의 관계가 아닌 정점과 간선 사이의 관계로 정의된다. Incidence matrix는 무향 그래프와 유향 그래프 모두에서 정의되지만, 여기에서 필요한 것은 유향 그래프의 incidence matrix이다.
유향 그래프의 incidence matrix는 정점이 \(n\)개이고 간선이 \(m\)개일 때, \(j\)번 간선이 \(i\)번 정점으로 들어오면 \((i, j)\) 원소가 \(1\)이고 \(j\)번 간선이 \(i\)번 정점에서 나가면 \(-1\), 둘다 아니면 \(0\)으로 정의되는 \(n\times m\) 행렬이다. 지금 그래프에는 방향이 없기 때문에, 우선 각 간선에 방향을 아무렇게나 주고 incidence matrix \(E\)를 구하면, Laplacian matrix가 아래와 같은 형태가 되는 것을 어렵지 않게 알 수 있다. (C–B formula 증명할 때처럼 인접 행렬로 경로의 수 구하는 방식 생각하면 된다.)
\[L=EE^T\]
이제 \(L\)에서 아무 행과 아무 열을 삭제한 \(L^*\)를 만들어야 하는데, 우선은 첫 번째 행과 첫 번째 열을 삭제했다고 가정하자. (증명을 따라가다 보면 왜 아무 행과 아무 열을 골라도 상관 없는지 이해될 것이다.) 그러면 \(E\)에서도 첫 번째 행을 날린 \(\bar{E}\)를 만들면 \(L^*=\bar{E}\bar{E}^T\)와 같이 쓸 수 있다. Cauchy–Binet formula에 의해 아래 식을 얻을 수 있다.
\[\det(L^*)=\sum_{I\subseteq{[m]\choose n-1}}\det(\bar{E}_{[n-1], I})\det(\bar{E}_{I,[n-1]}^T)=\sum_{I\subseteq{[m]\choose n-1}}\det(\bar{E}_{[n-1],I})^2\]
\(\bar{E}_{[n-1],I}\)에서 \(I\)의 의미를 생각해보면, 그래프의 간선 중 \((n-1)\)개를 고른 것이다. 스패닝 트리가 사이클이 없도록 \((n-1)\)개의 간선을 골라 만들어진 부분그래프임을 생각해보자.
\(\det(\bar{E}_{[n-1],I})\)를 전개했을 때 나오는 각 항의 순열 \(\sigma:[n-1]\to I\)는 \((n-1)\)개의 정점과 선택받은 \((n-1)\)의 간선의 '매칭'을 의미한다. 단 짝지을 간선이 정점에 연결되어 있어야 한다. 그렇지 않으면 incidence matrix 정의상 연결되어있지 않은 짝이 0이 되어 항이 사라지기 때문이다. \(I\)에 속한 각 간선에 대해 그 간선에 짝지어진 정점을 도착점으로 하도록 방향(주의: incidence matrix를 만들기 위해 임의로 부여했었던 방향과는 다르다)을 부여하면, 행렬식의 전개에서 0이 아닌 각 항은 \(E\)에서 삭제한 1번 정점(indegree 0)을 제외한 나머지 정점의 indegree가 1이 되도록 \(I\)의 간선에 방향을 부여한 것으로 해석할 수 있다. 즉, 이렇게 만든 방향 그래프에서는 정점 \(i\)로 들어가는 유일한 간선이 \(\sigma_i\)가 된다. 이 방향과 incidence matrix를 만들기 위해 임의로 부여했었던 방향과의 일치 여부에 따라 대응되는 항의 부호가 결정되게 된다. (이것과 별개로 \(\operatorname{sgn}\)의 존재도 잊어서는 안된다.)
만일 \(I\)가 스패닝 트리라면, \(E\)에서 삭제한 1번 정점을 트리의 루트로 간주할 때 나머지 \((n-1)\)개의 정점과 트리를 구성하는 \((n-1)\)개의 간선을 짝지을 방법이 유일하다. 정점과 그 부모를 잇는 간선을 짝지으면 된다. 이것이 의미하는 바는 \(\det(\bar{E}_{[n-1],I})=\pm 1\)이라는 것이다.
만일 \(I\)가 스패닝 트리가 아니라면 어떻게 될까? 이 경우 \(I\)에 포함된 (무향) 사이클이 반드시 존재한다. 이때 행렬식 전개의 각 순열 \(\sigma:[n-1]\to I\)에 대응되는 방향 그래프는 indegree가 모두 1 이하라는 특징 때문에 유향 사이클의 존재가 보장된다! (증명은 독자에게 맡긴다) 여기서 LGV를 증명할 때처럼 짝지어 상쇄시키는 아이디어를 사용한다. LGV에서는 교차점에서 두 경로의 진행 방향을 뒤바꿨다면, 여기서는 이 유향 사이클을 구성하는 간선의 방향을 뒤집어서 만든 방향 그래프와 짝짓는다.

이렇게 뒤집을 경우 incidence matrix를 만들 때 고정했던 방향과의 일치 여부가 전부 바뀌기 때문에 사이클의 길이가 홀수일 경우 부호가 뒤집힌다. 반면 \(\operatorname{sgn}\)의 경우 사이클의 길이가 짝수일 때 부호가 뒤집힌다! (이 역시 증명은 독자에게 맡긴다.) 결과적으로 행렬식의 전개에서 이렇게 짝지은 순열끼리 소멸하여 결과적으로 행렬식이 0이 된다.
최종적으로 \(\det(L^*)\)의 C–B formula에서 스패닝 트리에 대응되는 \(I\)만 1의 값을 남기게 되어 결과적으로 스패닝 트리의 개수와 같아지게 된다. 이렇게 matrix-tree 정리를 증명했다.
Laplacian matrix의 특징 덕분에 근본적으로는 같지만 약간은 다른 방법으로 스패닝 트리의 개수를 구할 수도 있다. 이 행렬은 Hermitian이기 때문에 대각화가 가능하고 중근을 포함해 \(n\)개의 실수 고윳값을 가진다. 자명한 고윳값으로 0을 가지는데, 0을 하나 제외한 나머지 고윳값을 모두 곱하고 \(n\)으로 나눠도 스패닝 트리의 개수를 구할 수 있다. 증명은 순수 선형대수학이고 어렵지 않으므로 수학에 자신 있다면 생각해 보는 것을 권한다.
마치며
3편에 걸쳐 PS를 위한 선형대수학 시리즈를 포스팅했다. 기본적인 내용부터 상당히 심도 있고 어려운 응용까지 다루었다. 이 정도면 PS에서 자주 등장하는 선형대수학 문제에 필요한 배경 지식은 대부분 정리했다고 생각한다. 초기 계획과 달리 matroid를 다루지 않았는데, linear matroid에 들어가는 선형대수학은 선형대수학 1편 수준의 지식으로 기본적이지만 그에 비해 matroid의 개념 자체가 쉬운 것이 아니기에 matroid의 핵심을 빼놓고 선형대수학의 응용으로만 작성하는 것은 의미가 없다고 생각했다. 추후 matroid 관련 주제를 작성하게 되면 그때 다룰 예정이다.
지금은 이 정도에서 마무리하지만, 재미있는 선형대수학의 응용에 대해 알게 되면 독립적으로 포스팅할 생각도 있다. 부족한 글을 읽어주신 독자 여러분께 감사의 말씀을 드리며...
연습문제
BOJ 18763: Knowledge-Oriented Problem
BOJ 18955: Determinant of a Graph
'Computer Science > 알고리즘' 카테고리의 다른 글
| Linear-time construction of the sieve of Eratosthenes (0) | 2022.09.11 |
|---|---|
| Linear Algebra in Problem Solving (2) (2) | 2022.09.02 |
| Linear Algebra in Problem Solving (1) (0) | 2022.08.31 |
| 2015 ACM-ICPC 한국 예선 F - 파일 합치기 (2) | 2020.05.02 |
| Link/Cut Tree (2) (7) | 2017.08.21 |



